Portfolio optimization of financial assets in Python from scratch

Portfolio optimization is a technique in finance which allow investors to select different proportions of different assets in such a way that there is no way to make a better portfolio under the given criterion. The criteria for optimization is generally to minimize the risk for a certain level of expected returns used as a constraint or maximize the returns while a certain level of risk used a constraint.

We write the portfolio optimization problem as


subject to



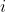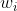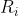Here are the number of assets in the portfolio,  are the weights (proportions) assigned to each   asset,   are the returns from each asset,  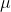are the average returns and  is the variance-covariance matrix. In simple words the above model can be understood as minimization of weighted variance-covariance matrix (or financial risk) with a certain level of returns 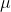 kept under constraint. The last constraint makes sure that all the weights are add up to 1.

Data collection and sources
I am going to use 6 assets in this example namely stocks, gold, foreign exchange (FOREX). bitcoins, real estate, and bonds. Bitcoins as assets are relatively new and less than a decade old but if you have not heard about them you can find an introduction of bitcoins here. The time period we are considering is between January 2015 till December 2016. I collected stocks data from yahoo finance API and bitcoin historical data from here.The data for remaining assets was collected using Quandl API from here. The data was collected using different APIs including Yahoo Finance, Quandl and was cleaned and merged such that it looks like the following

We see that different assets data has different scales so it must be normalized in order to make each asset comparable with each other. There is another way by which we can make this data comparable i.e. to calculate the daily returns for each asset which will make the range of our data from -1 to +1.  In Python this task is quite straight forward


Financial data is mostly compared using this method. After calculating the returns our data looks like the following and ready to be processed for optimization.




Portfolio optimization implementation in Python
We start optimizing our portfolio by doing some visualization so we have a general idea that how our data looks like. For this we'll simply plot our returns against the time and the following code will do that

We'll get the following graph as our output

We see that bitcoins show extremely high variations followed by bonds but on the other hand the returns are also extremely high verifying the assumption behind the modern portfolio theory. In the next stage we need to setup the returns and variance methods which will be used in optimization method. The idea behind building these methods is that we'll initialize our optimization with some random weights whose sum is 1. Then we'll update the weights by using some optimization method, say "SLSQP" in our example and will keep updating them until convergence. Following code will do that

The methods calc_exp_returns() and var_cov_matrix() have been implemented from the objective function above. In the objective function we have minimization of risk for which we implemented var_cov_matrix() and for the constraints we have calc_exp_returns()  and sum(weights) = 1 in the optimize() method. These constraints are set in the minimization problem under contraints parameter. For the purpose of performing analysis, we have used different expected returns values and determining how risk behaves if we vary expected returns. The list named exp_return_constraint contains different level of expected returns and we run the optimization as many times as we have elements in the list such that we'll get different risk levels for different expected returns.
The results will allow us to plot the efficient frontier for all feasible portfolios. Below is the method which plots the efficient frontier

From the graph we can see that higher expected returns leads to higher risk. In fact we see that as our expected returns are getting close to zero, our risk is also getting close to zero. Furthermore, the trajectory formed by the scatter plot is called "Efficient Frontier" in Finance and all the solutions or point lie on that trajectory are feasible for investors.
Finally, we need to see how weights are changing while we increase our expected returns. For this purpose we need to plot bar charts of weights for each level of expected returns.  Following code will do that

The legend of each bar chart shows the percentage risk and the optimal weights for assets on that level of risk. We can analyze from the graph that for higher level of returns the weights are biased towards bitcoins because its prices have increased significantly in the last few years. On contrary, when we decrease the level of expected returns, we see different variations in the weights but foreign exchange (forex) is the optimal due to its least risky nature. Furthermore, if we expect very low returns, say 0.01% , we see that the weights are biased towards forex. So if someone is willing to play very safe, then investing in forex is a good option but if someone is interested in earning more, he/she has to go with higher risk but then bitcoin would be a better investment choice.

Conclusion
In this tutorial I have tried to explain how we can find efficient portfolios and how to analyze them. With the current data for US and the given time period, we analyze that bitcoin is a good investment option for risk taking investors while forex is a good option for risk averse investors. This analysis is considered as a basic analysis in finance so a lot other factors can be incorporated in our model which might change our decision variable values to an extent.

The complete code for this example is available here on github.