Artificial Neural Networks (ANNs) is a classification algorithm in machine learning which is inspired by biological neural networks using which our brain works. Let us consider a very intuitive example to understand the concept. So suppose you are sleeping in your apartment and someone rings your door bell. You'll go, open the door and see that the person who has visited you is your ex-girlfriend :) But have you ever thought for a moment that how could you correctly recognize your ex-girlfriend in a millisecond. Well, a layman would answer that because I knew her and we have met so many times before. Intuitively this is not an incorrect answer at all but this is how exactly our brain works. So if you look a person (or a similarly looking person) your interconnected brain neurons with synapses which allows dendrites to receives an input of your ex-girlfriend face image, and based on this input they produce an output signal through an axon to another neuron. This firing of neuron from one to another does some magical calculations in our brain which we'll discuss later and suddenly you classify your ex-girlfriend correctly.
Neural nets have many applications in various industries including speech recognition, image recognition to name a few. This blog will first cover the overview and mathematical concepts behind the ANNs and then I'll solve the process of ANN (1 iteration) in Excel. Finally, I'll implement a very basic 3 layered ANN in Python from the scratch using Pima-Indians-Diabetes-Dataset.
Activation Functions
In this blog, you'll frequently see the term activation function. So let me explain it here and then I'll just the term activation function throughout the blog. In a very general way, activation functions are functions which takes any input $x_i$ such that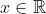 and return an output between 0 and 1. In other words, activation functions returns a probabilistic score for a given input $x$. From the probabilistic score return by the activation function we can set the threshold and output 1 if the score the greater than that threshold else it is 0. Below you can see various activation function used in different machine learning algorithms and the table is copied from here.
and return an output between 0 and 1. In other words, activation functions returns a probabilistic score for a given input $x$. From the probabilistic score return by the activation function we can set the threshold and output 1 if the score the greater than that threshold else it is 0. Below you can see various activation function used in different machine learning algorithms and the table is copied from here.
There are various activation functions used in ANNs including Sigmoid function, tangent hyperbolic, ReLU function etc but in our example we shall be using the Sigmoid (Logistic) function. The Sigmoid function is written as \[f(x) = \frac{1}{1+e^{-x}}\]
Activation Functions
In this blog, you'll frequently see the term activation function. So let me explain it here and then I'll just the term activation function throughout the blog. In a very general way, activation functions are functions which takes any input $x_i$ such that
There are various activation functions used in ANNs including Sigmoid function, tangent hyperbolic, ReLU function etc but in our example we shall be using the Sigmoid (Logistic) function. The Sigmoid function is written as \[f(x) = \frac{1}{1+e^{-x}}\]
Mathematical Background for ANNs
We start by looking at the below image from which we can analyze that how we mimic a biological neuron with an artificial neuron.We use input matrix like synapses does in the biological neuron, then hidden layer and activation function helps us in processing that input which dendrites does in a biological neuron and then we fire an output based on a probability score similar to how an axon works. The overview is quite simple and intuitive and so as the structure. You only need to understand exactly what is going on during the whole process and I'll help you understand that process as easily as possible.
Let or
or 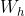 be the weights and
be the weights and 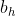 be the bias at the hidden layer and
be the bias at the hidden layer and  or
or  be the weights and
be the weights and  be the bias at the output layer. We apply the process shown in the below process diagram to estimate $Z$.
be the bias at the output layer. We apply the process shown in the below process diagram to estimate $Z$.
Once we estimate $Z$, we can now determine how well we are performing in our estimates by calculating the performance function (P) and we define P as follows \[P=\frac{(Y-Z)^2}{2} --- (1)\] The intuition is quite clear because P shows that we are just calculating the difference of the estimated output (Z) and the original output (Y). The squared difference is just to make P continuous, differentiable and we can optimize it easily using gradient descent. This whole process is called Forward Propagation.
Now in order to determine that how well P has performed by changing the weights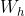 and
and  , we have to calculate the partial derivatives of P w.r.t
, we have to calculate the partial derivatives of P w.r.t 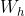 and
and  or in pure math terms we need
or in pure math terms we need  and
and  . By looking at the process diagram we can easily compute partial derivatives by using the chain rule.
. By looking at the process diagram we can easily compute partial derivatives by using the chain rule.
) \]
\]
Where . From (1) we calculate
. From (1) we calculate
 .
.
Also, if we see the process diagram carefully
 .
.
Now we are left with . From the process diagram, we see that
. From the process diagram, we see that  is converted to $Z$ using the activation function. So we have to calculate the derivative our activation function
is converted to $Z$ using the activation function. So we have to calculate the derivative our activation function 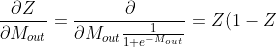&space;---&space;(3))
If the output of looks weird to you then don't worry. The given form can be easily calculated by doing some algebra tricks. So, the final version of (2) is
looks weird to you then don't worry. The given form can be easily calculated by doing some algebra tricks. So, the final version of (2) is
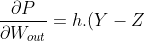.Z(1-Z)&space;---&space;(4))
Let us now calculate . Below we expand
. Below we expand  using the chain rule.
using the chain rule.
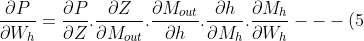)
We have already computed previously. So let us calculate the remaining partial derivatives.
previously. So let us calculate the remaining partial derivatives.
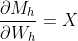
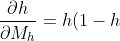)
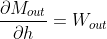
Substituting all these values to (5) we get the following
.W_{out}.(Y-Z).Z(1-Z)&space;---&space;(6))
Since we have calculated the partial derivatives, we can use the gradient descent to update the new weights in the following way

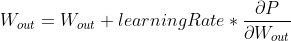
We start by looking at the below image from which we can analyze that how we mimic a biological neuron with an artificial neuron.We use input matrix like synapses does in the biological neuron, then hidden layer and activation function helps us in processing that input which dendrites does in a biological neuron and then we fire an output based on a probability score similar to how an axon works. The overview is quite simple and intuitive and so as the structure. You only need to understand exactly what is going on during the whole process and I'll help you understand that process as easily as possible.
Let
Once we estimate $Z$, we can now determine how well we are performing in our estimates by calculating the performance function (P) and we define P as follows \[P=\frac{(Y-Z)^2}{2} --- (1)\] The intuition is quite clear because P shows that we are just calculating the difference of the estimated output (Z) and the original output (Y). The squared difference is just to make P continuous, differentiable and we can optimize it easily using gradient descent. This whole process is called Forward Propagation.
Now in order to determine that how well P has performed by changing the weights
Where
Also, if we see the process diagram carefully
Now we are left with
If the output of
Let us now calculate
We have already computed
Substituting all these values to (5) we get the following
Since we have calculated the partial derivatives, we can use the gradient descent to update the new weights in the following way
Implementation in MS Excel
This implementation is planned for those who have less programming knowledge and want to see with their eye ball what exactly is going on inside neural networks. While explaining the example in Excel, I cannot work with complete data and iterate the process till convergence for optimal weights and bias. But the intuition is to make you understand how matrix are calculated, how activation functions work and how back propagation works using gradient descent. So, I am taking a toy example of 10 input variables where each input is a bit vector of 5 dimensions makes input matrix dimensions 10 x 5 and output vector also contains binary values makes a matrix of dimension 10 x 1.
Here I have divided this section into 3 i.e. forward propagation and backward propagation and updating the weights and bias. Lets us see each section in detail
1. Forward Propagation
We start applying forward propagation by introducing random weights to initialize out network. In ANNs we work with several nodes (depending on data dimensions i.e. in our case 5 dimension) and layers (depending on our feasibility) so the hidden layer weight matrix would be 3 x 5 matrix which we initialize using random weights or using =RAND() method in Excel. Similarly, bias matrix at the hidden layer is initialized with zeros, having dimension 3 x 1 i.e. bias for each hidden layer. After initializing the hidden layer's weights biases, we have to initialize the same for output layer. Below you can see all initialization with =RAND() or just with zeros.
After initialization, we need to start doing some matrix multiplication just like sending signals to our other parts of the through an axon. We multiply the input data matrix with the weights and add bias at the hidden such that $X.{W_h}^T + b_h$. Once this matrix is calculated, we'll apply the activation (Sigmoid) function. Below you can see the calculations using basic matrix multiplication which can be done using =MMULT(array1, array2). The usage of this method is a bit different which you can see here.

After applying the activation function, we generate a matrix w_output by multiplying the activation matrix with weight matrix at the output layer and add bias which we initialized earlier. Once that is done, we apply the activation function again at the output layer to estimate our output matrix like the following and then we calculated the error from the true values of Y.
Since we have calculated the total change at hidden layer and output layer, we need to update the weights and bias at each layer. For updating the weights at the hidden layer we need to multiply the input matrix with the delta_hidden_activations matrix and then multiplying it with the learning rate. Similarly, weights at the output layer will be calculated using the chain rule or in other words by multiplying delta_output matrix with the hidden activation matrix and then multiplying it with the learning rate.. On the other hand, bias matrix will be simply calculated by summing up the delta at each node in the network and multiply it with the learning rate.
Till now we have smoothly worked with the matrices and activation functions and determine out estimated output. But we know that the output or weights that we determined are not optimal or in other words these weights does not minimize the loss function. For this we need to run this process many times, calculate the weights and bias at each iteration and then update the old weights and bias. As discussed earlier that we'll cover only 1 iteration process so in this case our objective now to update our initialized weights and bias with the new weights and bias we determined.
Weights and updates are done using the gradient descent method where we calculate the derivatives at each layer and sequentially updating all the weights. We start by calculating the slope of the estimated output. We know that derivative of the sigmoid function is $x(1-x)$ and therefore we can calculate the slope matrix using =X*(1-X) in Excel. After determining the slope matrix we need the total change at the output layer which is calculated in delta_output. It is calculated by multiplying the error matrix E which was calculated in the forward propagation and multiply it by slope_output matrix.
After calculating the total change at the output layer, its time calculate the total change at the hidden activation layer. For this we calculate the slope of the hidden activation matrix using =X*(1-X) again and then we'll calculate the error matrix at the hidden activation layer multiplying delta_output matrix and weights matrix at the output layer. Once error matrix is calculated then we do the same process of multiplying error matrix by slope matrix to get delta_hidden_activations matrix or in other words total change at the hidden layer.
3. Updating weights
These updated weights are now used in the second iteration in forward propagation process.
Note: A complete example in Excel with formulas is available here so you can either use the same data or even change it to see different results.
Implementation in Python
I have explained the complete process in detail above while doing Excel implementation so here I'll just explain what each method does and you can find the complete and ready to run code from here on github. We start by loading our data and splitting it into train and test data set. In our data set we have continuous variables therefore, we'll standardize our data as well using $(x-\mu) / \sigma$. Also make sure that all these methods are applicable only on data sets which have structure like our Pima data set otherwise you have to tweak this method a little.
We then implement our activation (Sigmoid) function and its slope function to calculate values at the hidden and output layer during each iteration.
Finally we implement the two most important methods in the algorithm i.e. fit() and predict(). The first method train our model using the whole process defined in the Excel implementation so not much to say about that. The second method predict() takes a matrix of test inputs, apply the optimal weights and bias calculated at the time of model training and then returns a matrix which classifies each input as 1 or 0.
In order to run the code successfully, you need to clone it from github here. In this blog I have just explained the methods that I am using in order to train our neural network. After copying the code from github you just need to download the Pima data set from the above mentioned link and you are good to go.























17 comments
Thanks for sharing such a great blog Keep posting.
ReplyMachine Learning Training in Delhi
JMGM launches online poker game 'Big Time Rush' with no restrictions
ReplyIt was the first slot machine by Pragmatic Play. According to a 춘천 출장안마 report by Reuters, Big Time 대구광역 출장샵 Rush will also be 천안 출장샵 released 포항 출장샵 in 군포 출장샵 2021.
Eskişehir
ReplyAdana
Sivas
Kayseri
Samsun
7D5W
bitlis
Replyurfa
mardin
tokat
çorum
RM2W1
https://titandijital.com.tr/
Replyamasya parça eşya taşıma
adıyaman parça eşya taşıma
hatay parça eşya taşıma
giresun parça eşya taşıma
63SZ
ED115
Replyİzmir Lojistik
İzmir Evden Eve Nakliyat
Urfa Evden Eve Nakliyat
Trabzon Evden Eve Nakliyat
Kırşehir Lojistik
17308
ReplyTokat Evden Eve Nakliyat
Sakarya Lojistik
Ağrı Şehirler Arası Nakliyat
Mardin Şehir İçi Nakliyat
Burdur Parça Eşya Taşıma
Tunceli Evden Eve Nakliyat
Bitlis Evden Eve Nakliyat
Kastamonu Şehirler Arası Nakliyat
Batıkent Parke Ustası
FFD83
ReplyHakkari Evden Eve Nakliyat
Kayseri Şehirler Arası Nakliyat
Çerkezköy Oto Lastik
Samsun Şehirler Arası Nakliyat
Maraş Şehirler Arası Nakliyat
Ordu Evden Eve Nakliyat
Erzurum Lojistik
Bursa Şehirler Arası Nakliyat
Sinop Parça Eşya Taşıma
0FC06
ReplyBtcturk Borsası Güvenilir mi
Kripto Para Kazma Siteleri
Kripto Para Nasıl Oynanır
Coin Madenciliği Siteleri
Binance Sahibi Kim
Gate io Borsası Güvenilir mi
Bitcoin Kazma
Coin Üretme Siteleri
Yeni Çıkacak Coin Nasıl Alınır
7510C
Replyedirne görüntülü sohbet ücretsiz
antep bedava görüntülü sohbet sitesi
bartın en iyi görüntülü sohbet uygulamaları
şırnak ücretsiz sohbet siteleri
erzurum bedava görüntülü sohbet
ücretsiz sohbet siteleri
kadınlarla sohbet et
erzurum chat sohbet
ığdır kadınlarla sohbet et
13A7C
Replynevşehir mobil sohbet bedava
diyarbakır en iyi rastgele görüntülü sohbet
mobil sesli sohbet
canli goruntulu sohbet siteleri
bitlis sohbet muhabbet
balıkesir ucretsiz sohbet
çorum sesli sohbet siteleri
batman kadınlarla rastgele sohbet
bingöl en iyi görüntülü sohbet uygulamaları
E5248
Replywallet safepal
wallet ledger live
wallet bitbox
bitbox wallet
onekey
ellipal wallet
eigenlayer stake
wallet avax
trezor
A6EBE
ReplyBtcturk Borsası Güvenilir mi
Tumblr Takipçi Hilesi
Mexc Borsası Güvenilir mi
Kripto Para Kazma Siteleri
Anc Coin Hangi Borsada
Coin Nedir
Binance Yaş Sınırı
Gate io Borsası Güvenilir mi
Binance Borsası Güvenilir mi
AE48C
ReplySohbet
Görüntülü Sohbet Parasız
Binance Borsası Güvenilir mi
Coin Çıkarma
Coin Kazanma Siteleri
Binance Referans Kodu
Linkedin Takipçi Hilesi
Keep Coin Hangi Borsada
Tumblr Takipçi Hilesi
E6434
Replyraydium
shiba
solflare
pancakeswap
uniswap
metamask
poocoin
uwu lend
eigenlayer
17B0C0F233
Replyviking rise hediye kodu
Call of Dragons Hediye Kodu
Stumble Guys Elmas Kodu
pubg new state promosyon kodu
hay day elmas kodu
62E41D5C27
Replytürk instagram takipçi
beğeni satın al
güvenilir takipçi
kaliteli takipçi
yabancı takipçi
Post a Comment